%20for%20web.gif)
Our Lady Help of Christians Academy
%20for%20web.gif)
(Back to 6th Grade Home) (Back to 6th Math)
6th Grade Math - Archive
__________________________________________________
Due Monday, March 23rd
Math Assignment: "Integers in the Real World"
This short assignment will refresh your memories on our discussion about Integers.
Please write out the problems on your own separate sheet of paper. Be careful to be as neat as possible! (You know who I'm talking to! :) )
Due Wednesday, March 25th
Chapter 5-2, p. 153, 1-24 evens: You may do this one on paper or complete it ONLINE using the link provided.
Due Monday, April 6th
Workbook Lesson 5-2. This link shows the problems to be done. Complete them on your own lined paper. You do not have to copy the problem from the worksheet, but you do have to show your work (every step!) Be sure to write neatly! - COMPLETE THIS IF YOU HAVEN'T ALREADY TURNED IT IN - turn it in on Monday, April 6th
For Lesson 5-3, Look at the following illustration:
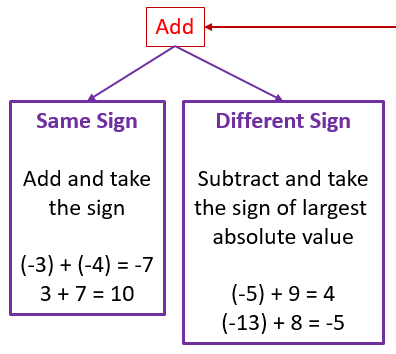
Adding integers when the signs are the same (both + or both -) is easy . . . add them together and keep the same sign in your answer.
Adding integers when the signs are different is also easy, but might seem tricky at first.
No matter which numbers have which signs . . . subtract the smaller number from the larger number and keep the sign of the larger number in your answer.
(Remember: "smaller number" and "larger number" here mean smaller and larger absolute value - but you know absolute value, so no problem! :) )
So look at the problem above that says (-13) + 8 = -5
The absolute value of the first integer |-13| is 13.
The absolute value of the second integer |8| is 8.
Subtract the smaller number from the larger number: 13 - 8 = 5.
What was the sign of the larger number? It was negative: (-13). So your answer is also negative: -13 + 8 = -5
Follow those steps to complete problems 1 - 18 (all) on the Chapter 5-3 Worksheet. Try problems 20 - 28 (evens) for extra credit!
Math Textbook Chapter 5-3. The link is just a reproduction of the pages from the 6th Math textbook, which all 6th graders already have at home. Do problems 1 and 2 on pg. 155, then also problems 4-32, evens only. COMPLETE THIS IF YOU HAVEN'T ALREADY TURNED IT IN - turn it in on Monday, April 6th
________________________________________________
Math Plan for the 4th Quarter
Dear Students,
We'll be focusing on these things during the 4th Quarter:
1. Addition, Subtraction, Multiplication, and Division of Integers (Remember: Integers are whole numbers and their opposites - . . . -3, -2, -1, 0, +1, +2, +3 . . .)
2, Addition, Subtraction, Multiplication, and Division of Decimals
3. Addition, Subtraction, Multiplication, and Division of Fractions
We'll include some word problems and work with variables, just to keep you on your toes! And we'll be sure to add the "problem of the day" and a handful of challenge problems for those who are interested!
Some of this will be brand new, some will be reminders and review of what you've learned before. If you can go into 7th grade with these concepts firmly under your belts, 7th grade math will be a breeze!
As always, you are most welcome to contact me by email, phone, text, or smoke signals . . . whatever works best for you.
We'll send out the Zoom class information as soon as that's finalized. I'm happy to have one-on-one Zoom sessions for anyone who is struggling, and I'll post my Zoom "office hours," where you can drop in to ask about your math lessons.
Best of luck, hope to see you all in person soon!
God bless,
Mrs. Eddy
________________________________________________
Assignments for April 20th - 24th
There will be 2 Exercises for Adding and Subtracting Integers and 2 Exercises for Multiplying and Dividing Integers. Printed copies of these 4 assignments were included with the 6th grade materials for the Monday, April 20th pick-up day, and are also available online below.
There are explanations in the math book for these concepts, but the explanations below are easier to understand. (This information was also printed and included in the pick-up materials.)
Assignment 2, Subtracting Integers
Assignment 3, Multiplying Integers
Assignment 4, Dividing Integers
SUBTRACTING INTEGERS
Remember when we learned the rules for adding integers (positive and negative whole numbers)? You can refresh your memory by checking the 6th Math Archive page, if you'd like.
We used this illustration to help explain the rules:

Well now we'll learn to SUBTRACT integers. The basic idea is this: change the subtraction problem to an addition problem, then follow the rules you've already learned for adding integers.
Look at the "Subtract" box in the picture below:
What does "Change to add the opposite" mean? It means that you're going to change the problem so that instead of subtracting, you're adding . . . and since you're going to do the opposite operation (adding now, instead of subtracting), you need to also make the sign for the number you were subtracting the opposite, too. Let's see an example.
Look at the problem in the "Subtract" box in the illustration above that says (-3) - (+4)
1. First, change that minus sign in between the numbers to a plus sign. So now you'll be doing the opposite operation, you'll be adding instead of subtracting.
2. Since you're doing the opposite operation now, you also need to change the sign of the +4 to its opposite, -4
So your new problem is (-3) + (-4)
Now you have an addition problem, so look at the "Add" box in the illustration above and follow the steps:
Are the signs for the 3 and the 4 the same or different? They're the same, they're both negative.
What do we do when the signs are the same? We add, and the answer takes the same sign: (-3) + (-4) = -7
Let's do one more! Look at the second problem in the "Subtract" box: (-5) - (-9)
1. First, change that minus sign in between the numbers to a plus sign. So now you'll be doing the opposite operation, you'll be adding instead of subtracting.
2. Since you're doing the opposite operation now, you also need to change the sign of the -9 to its opposite, +9
So your new problem is (-5) + (9)
Now you have an addition problem, so look at the "Add" box above and follow the steps:
Are the signs for the 5 and the 9 the same or different? They're different.
What do we do when the signs are different? We subtract the smaller number from the larger number and keep the sign of the larger number.
The absolute value of the first integer |-5| is 5.
The absolute value of the second integer |+9| is 9.
Subtract the smaller number from the larger number: 9 - 5 = 4.
What was the sign of the larger number? It was positive: (+9). So your answer is also positive: (-5) + (9) = +4
MULTIPLYING AND DIVIDING INTEGERS
Multiplying and dividing integers is SUPER EASY!
That's all you need to know!
If the signs are the same - that is, if they're both positive OR both negative - then multiply or divide as usual, and the sign of your final answer is positive.
If the signs are different - that is, if one is positive and the other is negative, doesn't matter which one is which - then multiply or divide as usual, and the sign of your final answer is negative.
Let's look at a couple of examples:
Same signs (answer is positive):
+3 x +5 = +15 or +15 ÷ +5 = +3
-3 x -5 = +15 or -15 ÷ -5 = +3
Different signs (answer is negative):
-3 x +5 = -15 or +15 ÷ -5 = -3
+3 x -5 = -15 or -15 ÷ +5 = -3
That's it! (Remember that any number, positive or negative, multiplied by zero equals zero.)
Assignments for April 27th - May 1st
We'll be moving on to a review of fractions this week. In order to work with fractions, we'll first do a little refresher on the following concepts.
The assignments below were printed and distributed with the pick-up materials on Monday, April 27th. You may view or download & print them by using the links.
These assignments are due Monday, May 4th. Explanations of each concept can be found in the lesson summaries below, and in the math textbook.
-Divisibility Rules (Chapter 6-1)
Assignment #1, Divisibility Rules
-Prime and Composite Numbers (Chapter 6-2)
Assignment #2, Prime and Composite Numbers
-Factor Trees (Chapter 6-3)
Assignment #3, Prime Factorization
-Equivalent Fractions (Chapter 6-4)
Assignment #4. Equivalent Fractions
(The assignment for this section was determined after our Zoom class this week.)
CHALLENGE PROBLEM: The difference between the digits of each of two 2-digit numbers is 7. The product of each two-digit number is 8. The sum of each two digit number is 9. What are the two numbers?
The Lesson Summaries below were printed and included with the pick-up materials, and may also be found in the math textbook.
DIVISIBILITY RULES: (Chapter 6-1 in your math textbooks.)
A number is divisible by another number if there is no remainder after you divide.
In the example below, we are dividing 351 by 9. When we work out the problem, we learn that 351 ÷ 9 = 39, and that there is no remainder:

We can use the Divisibility Rules to figure out which numbers to try when we divide. We're looking for numbers to use that will let us divide with no remainders.

Let's look at the number 3024, and see what numbers will divide into 3024 evenly - without leaving a remainder.
We'll use the chart above and test each number, starting with 2:

PRIME & COMPOSITE NUMBERS: (Chapter 6-2 in your math textbooks.)

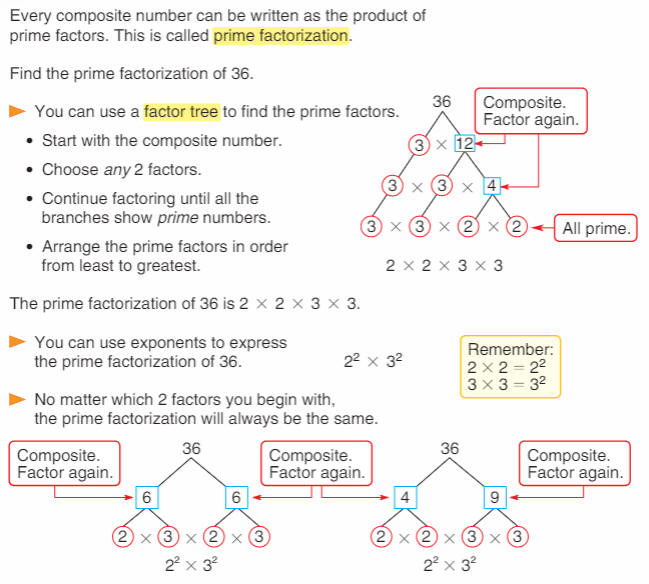
PRIME FACTORIZATION: (Chapter 6-3 in your math textbooks.)
6th Math Assignments for May 4th - 8th
These assignments are due Monday, May 11th. Paper copies were sent home with the pick-up packets. Digital copies are provided below, for viewing or downloading/printing.
Students may also submit their assignments online with the links provided.
This week we'll do a quick review of Greatest Common Factors, and use these GCF's to reduce fractions to their simplest forms.
We'll also convert Mixed Numbers into Improper Fractions, and Improper Fractions into Mixed Numbers.
Then we'll review finding Least Common Multiples, and use these LCM's to find common denominators in different fractions.
Explanations of each concept can be found in the lesson summaries below, and in the math textbook.
-Greatest Common Factors (Chapter 6-5)
Assignment #1 (OR use this link to submit online)
-Fractions in Simplest Form (Chapter 6-6)
Assignment #2 (OR use this link to submit online)
-Mixed Numbers and Improper Fractions (Chapter 6-7)
Assignment #3 (OR use this link to submit online)
-Least Common Multiples (Chapter 6-9)
Assignment #4 (OR use this link to submit online)
CHALLENGE PROBLEM: Mr. Eddy cut three lengths of board from one piece of lumber. The cut pieces were 2½ feet long, 6 feet long, and 3⅙ feet long. In the end, he had 2¼ feet left over. How long was the original board?
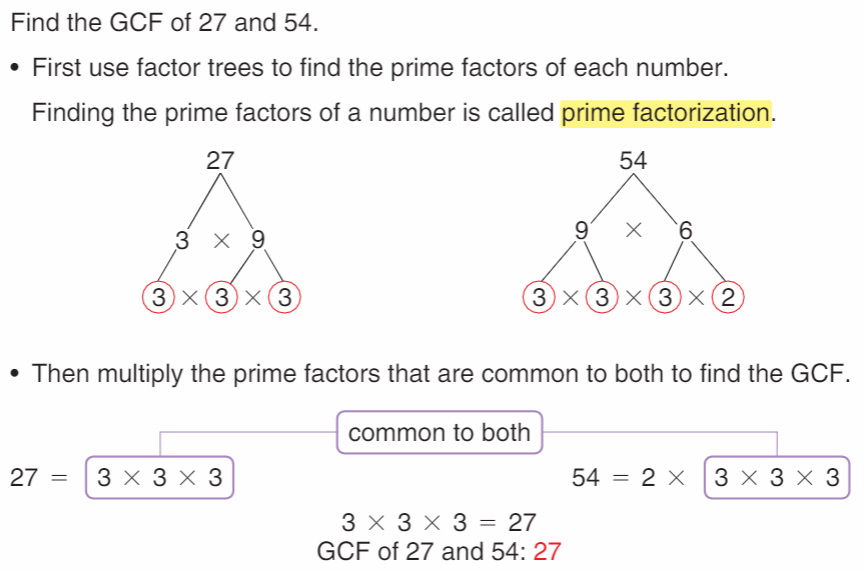
Finding the Greatest Common Factor (Chapter 6-5)
Remember: we can find the GCF two ways - making a list of factors, or doing a factor tree.
Example: Making a List

You may remember that when we did this in class, we found factors in pairs, starting with 1 and the number, then going to 2, 3, 4, etc.:
Factors of 12
(1, 12)
(2, 6)
(3, 4) - we're done finding factors of 12
We stopped at (3, 4) because the next largest number after 3 is 4 , and we already have 4 as a factor, so we know we're done.
Example: Doing a Factor Tree:
Putting Fractions in their Simplest Form (Chapter 6-6)
A fraction is in its "simplest form" or its "lowest terms" when the numerator (number on top) and the denominator (number on bottom) can't both be divided by any number bigger than 1.
Look at this example, where we are looking to find the simplest form of:
![]()

Remember last week when we said we can make "equivalent fractions" by multiplying the top and bottom by the same number, or by dividing the top and bottom by the same number? That's exactly what we're doing here - we're dividing the top and bottom by the same number. The number we're choosing to do this is the GCF.
After we divide the top and bottom by 4, we are left with
![]()
There is no number bigger than 1 that goes into 5 and also into 8, so we're done. That fraction is as simple as it can be!
Mixed Numbers and Improper Fractions (Chapter 6-7)
A fraction is a part of a whole. A fraction is "improper" when the numerator (the number on top, that tells how many pieces you have) is so large that you don't just have a fraction or part of a whole, you have a whole plus some extra pieces.
You might be asked to rewrite an "improper" fraction as a whole number plus those left-over pieces. A whole number plus pieces is called a mixed number.
Look at this example:
![]()
You have a bunch of fourths in that fraction - in fact, you have 38 fourths!
If 4 fourths makes 1 whole, you can see that you have a bunch of wholes in there.
38 ÷ 4 = 9, with a remainder of 2.
So you have 9 wholes in that fraction, plus 2 fourths left over.
If we put 2 fourths in the simplest form (2 and 4 are both divisible by 2), then we have 1 half.
So we can rewrite our improper fraction (38 fourths) as a mixed number (9 and 1 half):
This same example is in your book on page 190:

You may be asked to rewrite a "mixed number" as an improper fraction (which is the reverse of what we just did above). This example is also in your book on page 190:

We'll review going back and forth between improper fractions and mixed numbers in our Zoom class on Wednesday, so be ready to ask questions!
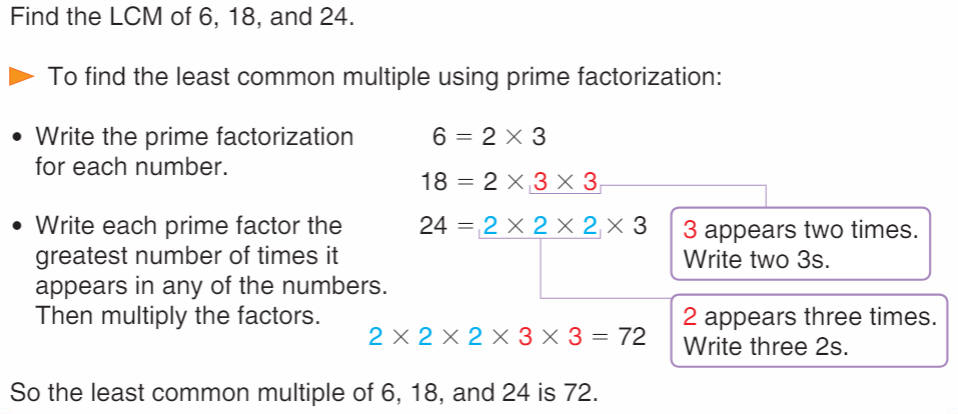
Finding the Least Common Multiple (Chapter 6-9)
Remember, the "least common multiple" of two or more numbers is the lowest number (not counting zero) that is a multiple of each of those numbers.
In class, we found the LCM's a couple of different ways.
First, by writing out the multiples of each number, in order, and stopping when we hit the first multiple they each had in common (the "least common multiple"):
Example: find the LCM of 6, 18, and 24 by multiplying each number by 1, then 2, then 3, etc.:
6 = 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, . . .
18 = 18, 36, 54, 72 . . .
24 = 24, 48, 72 . . .
We found that this method always works, but we might have to do A WHOLE BUNCH of multiplying before we happen to find the multiple that is the same. It's easy to make mistakes when you do many calculations. So we looked at another way, where we didn't have to do so many calculations - in this other way, we found the prime factors and used them to get the LCM.
So in our second way, we find the prime factors of each number by doing a factor tree, then make sure we take the MOST of each prime factor from each number to find the LCM:
We'll be using the LCM's to help us give different fractions a common denominator. Remember, the denominator is what tells you what kind of parts you have - halves, quarters, thirds, tenths, etc. Sometimes we'll need to make sure two or more fractions have the same denominator - like when we need to tell which fraction is bigger, or when we need to add or subtract them. The lowest common denominator is the LCM of the denominators - so once you have LCM's figured out, finding common denominators will be a breeze!